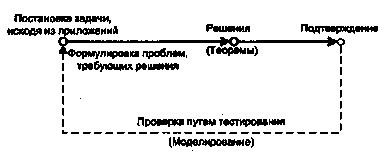
системы операций F, - {/,}, F2 - {f2,f3}, F3 ~ ifsJvfs), F4 - {UUUfi}, -, и тем самым построить иерархию операций Ftt.... Fp.
Для каждой операции в Fs можно определить количество и^ее выполнений при одной реализации алгоритма. Тогда сумма
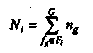 (2.21)
(2.21)будет представлять количество операций, выполняемых при одной реализации алгоритма, запрограммированного в терминах Ft. Характеристики элементной базы позволяют задать приближенное значение средней длительности т., операции в ВМ. С учетом этого время выполнения алгоритма на основе Fi составит Т.= τ , что дает
возможность поставить в соответствие иерархии систем операций F.....Fp затраты
времени на реализацию алгоритма Т,..., Тр, причем Т, < ... < Тр. Можно предположить, что минимум аппаратных затрат достигается при F„ принадлежит {Fr.., Fp}, обеспечит ющей время реализации алгоритма Тп, максимально близкое к заданному значению Удоп- В силу сказанного, выбор системы операций сводится к нахождению такой системы F„, для которой разность (Гдоп - Г„) имеет минимальное положительное значение.
Контрольные вопросы
1. Какие характеристики вычислительной машины охватывает понятие «архитектура системы команд»?
2. Охарактеризуйте эволюцию архитектур системы команд вычислительных машин.
3. В чем состоит проблема семантического разрыва?
4. Поясните различия в подходах по преодолению семантического разрыва, применяемых в ВМ с CISC- и RISC-архитектурами.
5. Какая форма записи математических выражений наиболее соответствует стековой архитектуре системы команд и почему?
6. Какие средства используются для ускорения доступа к вершине стека в ВМ со стековой архитектурой?
7. Чем обусловлено возрождение интереса к стековой архитектуре?
8. Какие особенности аккумуляторной архитектуры можно считать ее достоинствами и недостатками?
9. Какие доводы можно привести за и против увеличения числа регистров общего
назначения в ВМ с регистровой архитектурой системы команд?
10. Почему для ВМ с RISC-архитектурой наиболее подходящей представляется АСК с выделенным доступом к памяти?
11. Какую позицию запятой в формате с фиксированной запятой можно считать общепринятой?
12. Чем в формате с фиксированной запятой заполняются избыточные старшие разряды?
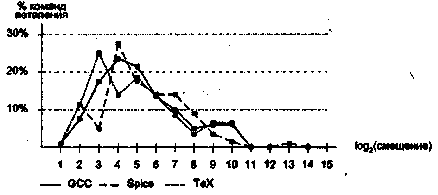
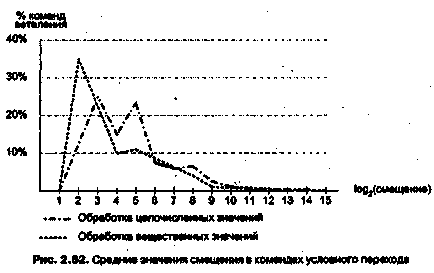

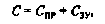
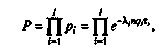 (2.13)
(2.13)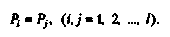 (2.14) Условие (2.14) можно переписать в ином виде:
(2.14) Условие (2.14) можно переписать в ином виде: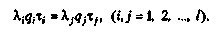 (2.15)
(2.15)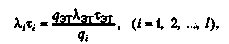 (2.16)
(2.16)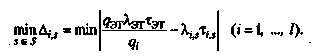 (2.17)
(2.17)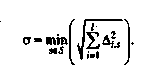 (2.18)
(2.18)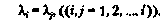

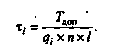

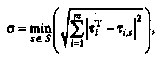
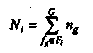 (2.21)
(2.21)