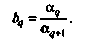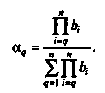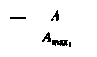148 Глава 3. Функциональная организация фон-неймановской ВМ
или строкой (одномерным массивом символов), что требует повторяющихся операций выборки и/или записи. Диаграмма отражает также возможность этапов прерывания и косвенной адресации.
Основные показатели вычислительных машин
Использование конкретной вычислительной машины имеет смысл, если ее показатели соответствуют показателям, определяемым требованиями к реализации заданных алгоритмов. В качестве основных показателей ВМ обычно рассматривают: емкость памяти, быстродействие и производительность, стоимость и надежность [25]. В данном учебнике остановимся только на показателях быстродействия и производительности, обычно представляющих основной интерес для пользователей.
Быстродействие
Целесообразно рассматривать два вида быстродействия: номинальное и среднее. Номинальное быстродействие характеризует возможности ВМ при выполнении стандартной операции. В качестве стандартной обычно выбирают короткую операцию сложения. Если обозначить через тсл время сложения, то номинальное быстродействие определится из выражения
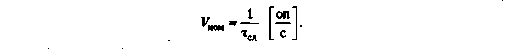
Среднее быстродействие характеризует скорость вычислений при выполнении эталонного алгоритма или некоторого класса алгоритмов. Величина среднего быстродействия зависит как от параметров ВМ, так и от параметров алгоритма и определяется соотношением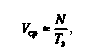
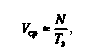
где Тэ — время выполнения эталонного алгоритма; Ν— количество операций, содержащихся в эталонном алгоритме.
Обозначим через щ число операций i-ro типа;/ — количество типов операций в алгоритме (г = 1, 2,...,/);tf — время выполнения операции i-ro типа.
Время выполнения эталонного алгоритма рассчитывается по формуле:
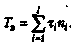 (3.1)
(3.1)Подставив (3.1) в выражение для Уср, получим
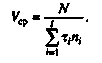
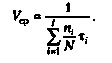
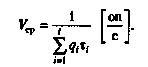 (3.4)
(3.4)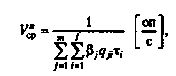 (3.5)
(3.5)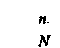
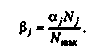 (3.6)
(3.6)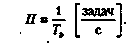
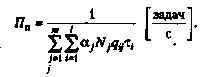 (37)
(37)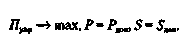
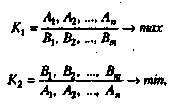
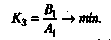 (3.10)
(3.10)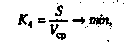 (3.11)
(3.11)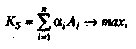 (3.12)
(3.12)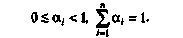 (3.13)
(3.13)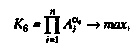 полагают равными единице.
полагают равными единице.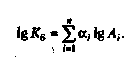 (3.15)
(3.15)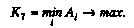 (3.16)
(3.16)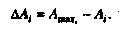
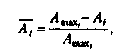 (3.18)
(3.18)