2 3 6 Глава 5. Память
бы арбитража при одномоментном обращении к одной и той же ячейке. В то же время есть и существенные отличия.
Первое состоит в том, что у микросхемы нет входов для указания адреса ячей­ки, занесение и считывание данных производится в порядке их поступления через одну входную точку и одну выходную.
Второе отличие связано с необходимостью слежения за состоянием очереди. Для этого в микросхеме имеются регистры-указатели адресов начала и конца оче­реди, а также специальные флаги, которые указывают на две ситуации: отсутствие данных (в этом случае блокируется считывание из микросхемы) и полное запол­нение памяти (блокируется запись).
Обнаружение и исправление ошибок
При работе с полупроводниковой памятью не исключено возникновение различ­ного рода отказов и сбоев. Причиной отказов могут быть производственные де­фекты, повреждение микросхем или их физический износ. Проявляются отказы в том, что в отдельных разрядах одной или нескольких ячеек постоянно считыва-ется 0 или 1, вне зависимости от реально записанной туда информации. Сбой — это случайное событие, выражающееся в неверном считывании или записи инфор­мации в отдельных разрядах одной или нескольких ячеек, не связанное с дефекта­ми микросхемы. Сбои обычно обусловлены проблемами с источником питания или с воздействием альфа-частиц, возникающих в результате распада радиоактив­ных элементов, которые в небольших количествах присутствуют практически в любых материалах. Как отказы, так и сбои крайне нежелательны, поэтому в боль­шинстве систем основной памяти содержатся схемы, служащие для обнаружения и исправления ошибок.
Вне зависимости от того, как именно реализуется контроль и исправление оши­бок, в основе их всегда лежит введение избыточности. Это означает, что контроли­руемые разряды дополняются контрольными разрядами, благодаря которым и воз­можно детектирование-ошибок, а в ряде методов — их коррекция. Общую схему обнаружения и исправления ошибок иллюстрирует рис. 5.15.
На рисунке показано, каким образом осуществляются обнаружение и исправ­ление ошибок. Перед записью М-разрядных данных в память производится их об­работка, обозначенная на схеме функцией «fi>, в результате которой формируется добавочный Ζ-разрядный код. В память заносятся как данные, так и этот вычис­ленный код, то есть (М + ^-разрядная информация. При чтении информации по­вторно формируется Ζ-разрядный код, который сравнивается с аналогичным ко­дом, считанным из ячейки. Сравнение приводит к одному из трех результатов:
•   Не обнаружено ни одной ошибки. Извлеченные из ячейки данные подаются на выход памяти.
•   Обнаружена ошибка, и она может быть исправлена. Биты данных и добавоч­ного кода подаются на схему коррекции. После исправления ошибки в М-раз­рядных данных они поступают на выход памяти.
•  Обнаружена ошибка, и она не может быть исправлена. Выдается сообщение о неисправимой ошибке.
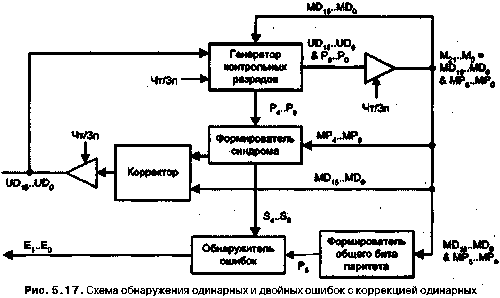
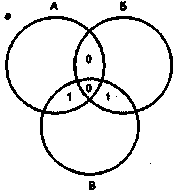Обнаружение и исправление ошибок 2 3 7
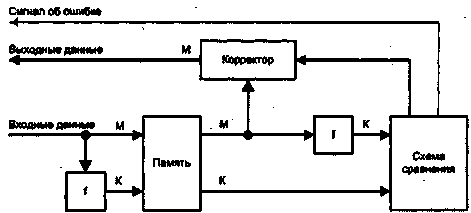
Рис. 5.15 Общая схема обнаружения и исправления ошибок [200]
Коды, используемые для подобных операций, называют корректирующими ко­дами или кодами с исправлением ошибок.
Простейший вид такого кода основан на добавлении к каждому байту инфор­мации одного бита паритета. Бит паритета — это дополнительный бит, значение которого устанавливается таким, чтобы суммарное число единиц в данных, с уче­том этого дополнительного разряда, было четным (или нечетным). В ряде систем за основу берется четность, в иных — нечетность. Для 64-разрядного слова требу­ется восемь битов паритета, то есть ячейка памяти должна хранить 36 разрядов. При записи слова в память для каждого байта формируется бит паритета. Это мо­жет быть сделано с помощью схемы в виде дерева, составленного из схем сложе­ния по модулю 2. При чтении из памяти выполняется аналогичная операция над считанными информационными битами, а ее результат сравнивается с битом па­ритета, вычисленным при записи и хранившимся в памяти. Метод позволяет об­наружить ошибку, если исказилось нечетное количество битов. При четном числе ошибок метод неработоспособен. К сожалению, фиксируя ошибку, данный способ кодирования не может указать на ее местоположение, что позволило бы внести исправления, в силу чего его называют кодом с обнаружением ошибки (ED С — Error Detection Code).
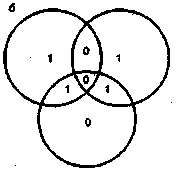
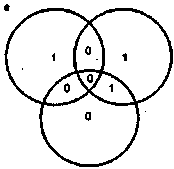
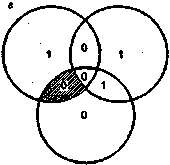
В основе корректирующих кодов лежит достаточно простая идея [39]. Для кон­троля двоичного информационного кода длиной Мбит добавим к ней Хдополни-тельных контрольных разрядов так, что общая длина последовательности теперь будет равна М + К разрядам. В этом случае из возможных N= Т+к комбинаций интерес представляют только L = Т последовательностей, которые называют раз­решенными. Оставшиеся iV- L последовательностей назовем запрещенными. Если при обработке (записи в память, считывании или передаче) разрешенной кодовой последовательности произойдут ошибки и возникнет одна из запрещенных после­довательностей, то тем самым эти ошибки обнаруживаются. Если же ошибки пре­вратят одну разрешенную последовательность в другую, то такие ошибки не могут быть обнаружены. Для исправления ошибок необходимо произвести разбиение множества запрещенных последовательностей на L непересекающихся подмно-
2 3 8 Глава 5. Память
жеств и каждому подмножеству поставить в соответствие одну из разрешенных последовательностей. Тогда, если была принята некоторая запрещенная последо­вательность, входящая в одно из подмножеств, считается, что передана разрешен­ная последовательность, соответствующая этому подмножеству, производится за­мена, чем и исправляется возникшая ошибка.
Простейший вариант корректирующего кода также может быть построен на базе битов паритета. Для этого биты данных представляются в виде матрицы, к каждой строке и столбцу которой добавляется бит паритета. Для 64-разрядных данных этот подход иллюстрирует табл. 5.1 [200]. Здесь D — биты данных, С— столбец битов паритета строк, К— строка битов паритета столбцов, Р— бит паритета, кон- ' тролирующий столбец С и строку К. Таким образом, к 64 битам данных нужно до­бавить 17 бит паритета: по 8 бит на строки и столбцы и один дополнительный бит для контроля строки и столбца битов паритета. Если в одной строке и одном столбце обнаружено нарушение паритета, для исправления ошибки достаточно просто инвертировать бит на пересечении этих строки и столбца. Если ошибка паритета выявлена только в одной строке или только одном столбце либо одновременно в нескольких строках и столбцах, фиксируется многобитовая ошибка и формирует­ся признак невозможности коррекции.
Таблица 5.1. Формирование коррелирующего кода для 64-битовых данных
0
1
2
3
4
5
в
7
0
А,
А
А
о,
А
А
А
А
С0
1
Др
А
Ас
А.
А3
Аз
А«
А=5
с,
2
А«
Ох,
А*
Ав
А»
Αι
Аз
Аз
с,
3
А*
а*
Ав
Ат
А»
А,
Ао
At
С3
4
А»
Аз
А*
А*
А,
Ат
А»
Аэ
с,
5
А»
А,
At
As
А*
А*
А«
А,
с*
в
А*
Аг>
А.
А,
As
Аз
А,
As
с6
7
А*
D»
А*
А»
Ао
А.
А*
Аз
с7
К>
*.
Ъ
к3
Ъ
К,
К
К,
р
Недостаток рассмотренного приема в том, что он требует большого числа до­полнительных разрядов. Более эффективным представляется код, предложенный Ричардом Хэммингом и носящий его имя (код Хэмминга). Логику этого кода для четырехразрядных слов (М=4) иллюстрирует диаграмма Венна1, приведенная на рис. 5.16
Три пересекающихся окружности образуют семь сегментов. Четырем битам данных назначаются внутренние сегменты (см. рис. 5.16, а), а остальные сегменты заполняются битами паритета. Биты паритета выбираются таким образом, чтобы
1 Диаграмма Венна — это графическое представление операций над множествами, где множества обо­значаются замкнутыми областями, содержащими.внутри.себя все элементы этих множеств. Диаграм­ма используется для отображения логических отношений между элементами множеств. Так, заштри­хованная область на рис. 5.16, г есть представление функции пересечения множеств А, Б и В (математически это записывается как А п Б п В).
Обнаружение и исправление ошибок 2 3 9
Рис. 5.16. Иллюстрация кодаХэмминга для четырехразрядного слова
общее число единиц в каждой окружности было четным (см. рис. 5.16,6). Так, посколь­ку окружность А содержит одну единицу, бит паритета для нее принимается равным 1. Теперь, если в результате ошибки изменится один из битов данных (см. рис. 5.16, в), это легко выявить. Путем проверки паритета обнаруживаются несоответствия в окружностях А и В. Для окружности Б несоответствия нет. Только один из семи сегментов присутствует в окружностях А и В и отсутствует в Б, и ошибка может бьпь исправлена за счет изменения бита в этом сегменте (см. рис. 5.16, г).
Для пояснения концепции, положенной в основу кода Хэмминга, построим код, обнаруживающий и исправляющий однобитовые ошибки в 8-разрядных словах (пример взят из [47]).
Сначала определим требуемую длину корректирующего кода. В соответствии с рис. 5.15, на вход схемы сравнения поступают два Ζ-разрядных значения. Срав­нение производится путем поразрядной операции «исключающее ИЛИ» (сложе­ние по модулю 2) над входными кодами. Результатом является так называемое слово синдрома. В зависимости от того, было ли совпадение входных кодов или нет, соответствующий бит синдрома будет равен 0 или 1.
Слово синдрома состоит из ^разрядов, то есть его возможные значения лежат в диапазоне от 0 до ί - 1. Значение 0 соответствует случаю, когда ошибки не об­наружено, остальные ί -\ случая свидетельствуют о наличии ошибки и указывают
2 4 0 Глава 5. Память
на ее местоположение. Поскольку ошибка может возникнуть в любом из М битов данных или ^контрольных битов, мы должны иметь 2е - 1 > М + К. Это выраже­ние позволяет определить число битов, необходимое для исправления одиночной ошибки в Af-разрядных данных.
В табл. 5.2 приведено количество корректирующих разрядов, нужное для конт­роля данных различной разрядности. Из таблицы видно, что для 8-разрядных слов требуется четыре корректирующих разряда.
Для удобства будем формировать четырехразрядный синдром со следующими характеристиками:
•   Если синдром содержит все нули, значит, не обнаружено ни одной ошибки.
•   Если синдром содержит единственную единицу в одном из разрядов, это озна­чает, что выявлена ошибка в одном из четырех корректирующих разрядов и ни­какой коррекции не требуется.
•   Если в синдроме в единичное состояние установлены несколько битов, то чис­ленное значение синдрома соответствует позиции ошибки в данных, для исправ­ления которой необходимо инвертировать бит в этой позиции.
Таблица 5.2. Количество корректирующих разрядов, используемое в кодеХэмминга
Разрядность
Исправление одиночной ошибки
Исправление одиночной ошибки Обнаружение двойной ошибки
Контрольные биты
% увеличения длины кода
Контрольные биты
% увеличения длины кода
8
4
50
5
62,5
16
5
31,25
6
37,5
32
6
18,75
7
21,875
64
7
10,94 "
8
12,5
128
8
6,25
9
7,03
256
9
3,52
10
3,91
Под контрольные разряды отводятся те биты, чьи позиционные номера пред-ставляютсобой степень числа 2 (табл. 5.3). Отдельный контрольный разряд от­вечает за определенные биты данных. Так, разрядная позиция п контролируется теми битами Pj, которые делают справедливым соотношение Σ; = п. Например, раз­ряд данных с позиционным номером 710 (01112) контролируется битами 4, 2 и 1 (7 - 4 + 2 + 1), а разряд с номером 1010 (10102) - битами 8 и 2 (10 - 8 + 2).
Таблица 5.3. f Распределение разрядов 12-разрядного слова между данными
и контрольным кодом
Десятичный
12
11
10
9
8
7
6
5
4
3
2
1
номер
позиции
Двоичный
1100
1011
1010
1001
1000
0111
0110
0101
0100
0011
0010
0001
код номера
позиции
Обнаружение и исправление ошибок 24 1
Биты данных
А
Ь,
А
А
А
А
D,
А
Контрольные биты
Л
Л
Р*
Л
Таким образом, для рассматриваемого случая значения контрольных разрядов вычисляются по следующим правилам:
pt - А ф А Ф А © А © А; р2 - а © А $ А © А © А;
P„-A©A®A®A;
ps-as©a©A®A·
Проверим корректность такой схемы на примере. Пусть входной крд равен 00101011, где разряду Z), соответствует правая цифра. Контрольные разряды вы­числяются следующим образом:
Λ-ΑΦΑΦΑΦΑΦΑ-ιφιφιφοφο-Ι; рг - а ф А © А © А © А -1 © о © 1 Ф 1 Ф о -1;
.р, - А © А ф А © А ~ ! © о Ф 1 Ф 0 - 0; я8-АФА®А7ФА"ОФ1®о®о~1·
Предположим, что данные в бите 3 содержат ошибку и там вместо 0 находит­ся 1. После пересчета контрольных разрядов имеем
/γ-ΑΦΑ©Α®Α5ΦΑ-1Φ1Φ1Φ0Φ0-1;
/у - А ® А3 © А ® А ® А7 - 1 Ф 1 Ф 1 Ф 1 Ф 0 - 0;
Р4'-А©А©А©А8-1Ф1Ф1Ф0-1;
iy=As®A®A®A~o®i®o®0"i·
Путем сложения по модулю двух результатов старой и новой проверок полу­чим слово синдрома (S S S SJ:
ί,-ρ,ΦΡ,'-ΐΦΐ-θ;
52-Р2ФР;-1Ф1-0; ^-Р4ФР/-1Ф1-0;
Л-Л®^' -1Ф1-0.
Результат 01102 (610) означает, что в разряде 6, содержащем третий бит данных, присутствует ошибка.
Описанный код называется кодом с исправлением одиночной ошибки (SEC — Single Error Correcting). В большинстве микросхем памяти используется код с ис­правлением одиночной и обнаружением двойной ошибки (SECDED — Single Error Correcting, Double Error Detecting). Из табл. 5.2 видно, что, по сравнению с SEC, такой код требует одного дополнительного контрольного разряда.
Коды с исправлением ошибок применяются в большинстве ВМ. Например, в ос­новной памяти ВМ типа IBM ЗОхх используется 8-разрядный код SECDED на каж­дые 64 бита данных, то есть емкость памяти примерно на 12% больше, чем имеет в своем распоряжении пользователь. В ВМ типа VAX на каждые 32 разряда данных добавлен 7-разрядный код SECDED, следовательно, избыточность составляет 22%.
242 Глава 5. Память
Структура одного из вариантов построения устройства для обнаружения оди­нарных и двойных ошибок с коррекцией одинарных ошибок приведена на рис. 5.17. Схема предназначена для контроля 16-разрядных данных и размещается между процессором и памятью. Из табл. 5.2 видно, что код SECDED предполагает шесть дополнительных разрядов. Таким образом, из процессора и в процессор поступа­ют 16-разрядные коды (UD15...UD), а в память заносятся 22-разрядные данные (М21... М0). Хранящаяся в ячейках памяти информация состоит из 16 бит инфор­мации (MD15... MD) и 6 контрольных битов (МР5... МР). В последующем первые буквы в обозначении разрядов могут быть опущены, при этом D будет означать информационный разряд кода, а Р — контрольный разряд.
Система размещения основных и контрольных разрядов была рассмотрена ра­нее, и для данной схемы она приведена в табл. 5.4.
Таблица 5.4. Распределение информационных и контрольных разрядов в 22-разрядном слове
Номер позиции
22
21
20
19
18
17
16
15
14
13
12
Биты данных
А*
D%t
Аэ
Αι
А.
А»
А
А
А
Контрольные биты
Р*
Л
Номер позиции
И
10
9
8
7
6
5
4
3
2
1
Биты данных
А
А
А
А
А
А
А
Контрольны* биты
Р,
t
Р,
Л
п
Контрольные разряды Р4... Р0 вычисляются по стандартной схеме кода Хэмминга:
р0=о,5едэФА,еА0ФД(ФД1фД|ФА1®А®А>;
Р, - Дз Ф Аг © Ао Ф А, Ф Д Ф А5ф Αι Θ Д Ф Д,;
рг - д5 ф А, © А» ф А> © А, ф А ф А, ф а2 θ а,;
Рэ-Д0ФДФА8ФА7ФАФДФА4;
Р4 - As Ф Аи Ф Аз Ф Аг Ф Aj.
Особенность рассматриваемой схемы состоит в способе формирования конт­рольного разряда Ру Он вычисляется путем суммирования по модулю 2 всех ос­тальных 21 разрядов кода (Dly.. D0 и МР4... МР). По мнению авторов рассматри­ваемой схемы, это облегчает фиксацию факта неисправимой двойной ошибки. При чтении из памяти формирователем синдрома вычисляется синдром S4... S0:
50-РоФЛ/Р0;
5,-Ρ,ΦΛ/Λ;
5г-РгФМР2\
53-Р3ФЛ/Р3;
ί,-Ρ,ΦΜΡ,.
Здесь Р4... Р0 — контрольные разряды, вычисленные генератором контрольных разрядов на основании информационных битов считанного из памяти кода (MD15... MD). МР5... МР0 — такие же контрольные разряды, полученные тем же генерато­ром, но перед записью информации в память и хранившиеся там вместе с основ-
Обнаружение и исправление ошибок 2 4 3
ной информацией. Если синдром не равен нулю, то он указывает на позицию иска­зившегося бита при одиночной ошибке. С учетом контрольного разряда Р5 воз­можны четыре ситуации, показанные в табл. 5.5.
Таблица 5.5.
Обнаружение ошибок
Синдром
Р5
Тип ошибки
Примечания
0
0
Ошибки нет
*0
1
Одиночная ошибка
Корректируемая: синдром указывает на позицию искаженного разряда
*0
0
Двойная ошибка
Неисправимая
0
1
Ошибка в контрольном разряде
Искажен контрольный разряд Р5, и он быть откорректирован
может
Сигнал Чт/Зп на схеме определяет выполняемую операцию. Чт/Зп = 1 означает чтение из памяти, а Чт/Зп = 0 — запись в память.
Проанализировав полученный синдром и разряд Р5, обнаружитель ошибки фор­мирует двухразрядный код ошибки Εβ0 (табл. 5.6).
Таблица 5.6. Кодирование ошибок
Код ошибки (Е1 ,ЕО)
Описание
00
Ошибки нет
01
Одиночная ошибка — исправимая .
10
Двойная ошибка—неисправимая
п
Ошибка в контрольном разряде — исправимая
Hosted by uCoz