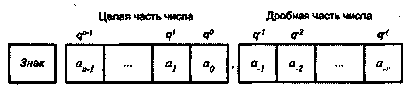
64 Глава 2. Архитектура системы команд
обеспечивают передачу в арифметико-логическое устройство операндов, храня­щихся в двух регистрах общего назначения. Третья служит для занесения резуль­тата в выделенный для этого регистр. Эти же шины позволяют загрузить в регистры содержимое ячеек основной памяти и сохранить в ОП информацию, находящую­ся в РОН.
Рис. 2.9. Архитектура вычислительной машины с выделенным доступом к памяти
АСК с выделенным доступом к памяти характерна для всех вычислительных машин с RISC-архитектурой. Команды в таких ВМ, как правило, имеют длину 32 бита и трехадресный формат. В качестве примеров вычислительных машин с выделенным доступом к памяти можно отметить HP PA-RISC, IBM RS/6000, Sun SPARC, MIPS R4000, DEC Alpha и т. д. К достоинствам АСК следует отнести про­стоту декодирования и исполнения команды.
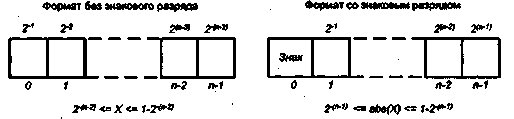
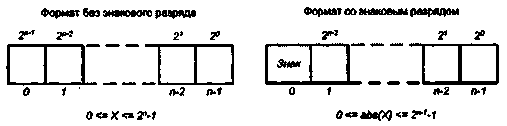
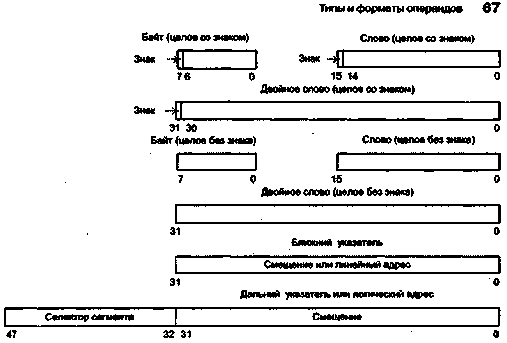
Типы и форматы операндов
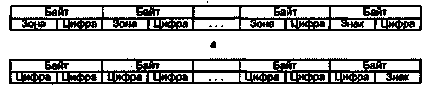
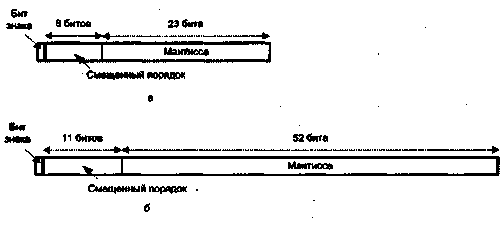
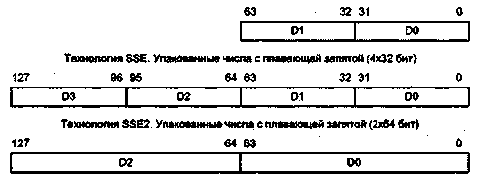
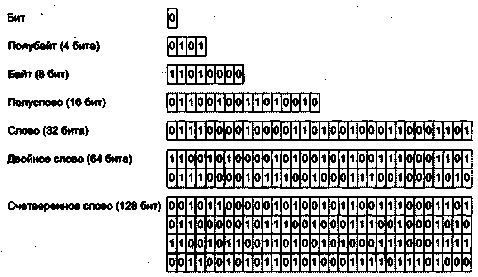
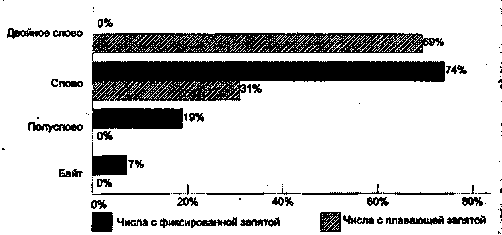
Машинные команды оперируют данными, которые в этом случае принято назы- ; вать операндами. К наиболее общим (базовым) типам операндов можно отнести: ■ адреса, числа, символы и логические данные. Помимо них ВМ обеспечивает об­работку и более сложных информационных единиц: графических изображе--ний, аудио-, видео- и анимационной информации. Такая информация является производной от базовых типов данных и хранится в виде файлов на внешних запо- \ минающих устройствах. Для каждого типа данных в ВМ предусмотрены опреде­ленные форматы.                                                                                         ■ ';
Типы и форматы операндов 65
Числовая информация
Среди цифровых данных можно выделить две группы:
•   целые типы, используемые для представления целых чисел;
•   вещественные типы для представления рациональных чисел.
В рамках первой группы имеется несколько форматов представления числен­ной информации, зависящих от ее характера. Для представления вещественных чисел используется форма с плавающей запятой.
Числа в форме с фиксированной запятой
Представление числаХв форме с фиксированной запятой (ФЗ), которую иногда называют также естественной формой, включает в себя знак числа и его модуль в q-ичном коде. Здесь q — основание системы счисления или база. Для современных ВМ характерна двоичная система (q = 2), но иногда используются также восьмерич­ная (<7 = 8) или шестнадцатеричная (q = 16) системы счисления. Запятую в записи числа называют соответственно двоичной, восьмеричной или шестнадцатеричной. Знак положительного числа кодируется двоичной цифрой 0, а знак отрицательно­го числа — цифрой 1.
Числам с ФЗ соответствует запись видаХ= ±<2п_1...а1а0а_,<2_2...а_г Отрицатель­ные числа обычно представляются в дополнительном коде. Разряд кода числа, в ко­тором размещается знак, называется знаковым разрядом кода. Разряды, где распола­гаются значащие цифры числа, называются цифровыми разрядами кода. Знаковый разряд размещается левее старшего цифрового разряда. Положение запятой оди­наково для всех чисел и в процессе решения задач не меняется. Хотя запятая и фик­сируется, в коде числа она никак не выделяется, а только подразумевается. В об­щем случае разрядная сетка ВМ для размещения чисел в форме с ФЗ имеет вид, представленный на рис. 2.10, где п разрядов используются для записи целой части числа и г разрядов — для дробной части.
Рис. 2.10. Формат представления чисел с фиксированной запятой
При заданных значениях п и г диапазон изменения модулей чисел, коды кото­рых могут быть представлены в данной разрядной сетке, определяется соотноше­нием
(Г-И-ί"-?-*.
Если число является смешанным (содержит целую и дробную части), оно обра­батываются как целое, хотя и не является таковым (в этом случае применяют тер­мин масштабируемое целое). Обработка смешанных чисел в ВМ встречается крайне редко. Как правило, используются ВМ с дробной (п = 0) либо целочисленной (г = 0) арифметикой.
3 3at470
66 Глава 2. Архитектура системы команд
При фиксации запятой перед старшим цифровым разрядом (рис. 2.11) могут быть представлены только правильные дроби. Для ненулевых чисел возможны два варианта представления (нулевому значению соответствуют нули во всех разря­дах): знаковое и беззнаковое. Фиксация запятой перед старшим разрядом встре­чалась в ряде машин второго поколения, но в настоящее время практически отжи­ла свое.
Рис. 2.11. Представление дробных чисел в формате ФЗ
При фиксации запятой после младшего разряда представимы лишь целые чис­ла. Это наиболее распространенный способ, поэтому в дальнейшем понятие ФЗ будет связываться исключительно с целыми числами, а операции с числами в форме ФЗ будут характеризоваться как целочисленные. Здесь также возможны числа со знаком и без знака (рис. 2.12):
Рис. 2.12. Представление целыхчисел в формате ФЗ
На рис. 2.13 приведены целочисленные форматы с фиксированной запятой, принятые в микропроцессорах фирмы Intel.
Целые числа применяются также для работы с адресами. На рис. 2.13 это 32-разрядный формат ближнего и 48-разрядный формат дальнего указателей.
Представление чисел в формате ФЗ упрощает аппаратурную реализацию ВМ и сокращает время выполнения машинных операций, однако при решении задач необходимо постоянно следить за тем, чтобы все исходные данные, промежуточ­ные и окончательные результаты не выходили за допустимый диапазон формата, иначе возможно переполнение разрядной сетки и результат вычислений будет не­верным.
Упакованные целые числа
В АСК современных микропроцессоров имеются команды, оперирующие целыми числами, представленными в упакованном виде. Связано это с обработкой муль-
Рис. 2.13. Целочисленные форматы микропроцессоров фирмы Intel
тимедийной информации. Формат предполагает упаковку в пределах достаточно длинного слова (обычно 64-разрядного) нескольких небольших целых чисел, а со­ответствующие команды обрабатывают все эти числа параллельно. Если каждое из чисел состоит из четырех двоичных разрядов, то в 64-разрядное слово можно поместить до 16 таких чисел. Неиспользованные разряды заполняются нулями. В микропроцессорах фирмы Intel, начиная с Pentium ММХ, присутствуют спе­циальные команды для обработки мультимедийной информации (ММХ-коман-ды), оперирующие целыми числами, упакованными в квадрослова (64-разрядные слова). Предусмотрены три формата (рис. 2.14): упакованные байты (восемь 8-раз­рядных чисел); упакованные слова (четыре 16-разрядных числа) и упакованные двойные слова (два 32-разрядных числа).
Рис. 2.14. Форматы упакованных целых чисел в технологиях ММХ и 3DNow!
68 Глава 2. Архитектура системы команд
Байты в формате упакованных байтов нумеруются от 0 до 7, причем байт 0 рас­полагается в младших разрядах квадрослова. Аналогичная система нумерации и размещения упакованных чисел применяется для упакованных слов (номе­ра 0-3) и упакованных двойных слов (номера 0-1).
Идентичные форматы упакованных данных применяются также в другой тех­нологии обработки мультимедийной информации, предложенной фирмой AMD. Эта технология носит название 3DNow!, а реализована в микропроцессорах дан­ной фирмы.
Десятичные числа
В ряде задач, главным образом, учетно-статистического'характера, приходится иметь дело с хранением, обработкой и пересылкой десятичной информации. Осо­бенность таких задач состоит в том, что обрабатываемые числа могут состоять из различного и весьма большого количества десятичных цифр. Традиционные ме­тоды обработки с переводом исходных данных в двоичную систему счисления и об­ратным преобразованием результата зачастую сопряжены с существенными на­кладными расходами. По этой причине в ВМ применяются иные специальные формы представления десятичных данных. В их основу положен принцип коди­рования каждой десятичной цифры эквивалентным двоичным числом из четырех битов (тетрадой), то есть так называемым двоично-десятичным кодом (BCD — Binary Coded Decimal).
б
Рис. 2.15. Форматы десятичных чисел: а — зонный; б — уплотненный
Используются два формата представления десятичных чисел (все числа рас­сматриваются как целые): зонный (распакованный) ^уплотненный (упакованный). В обоих форматах каждая десятичная цифра представляется двоичной тетрадой, то есть заменяется двоично-десятичным кодом. Из оставшихся задействованных шести четырехразрядных двоичных комбинаций (24 = 16) две служат для кодиро­вания знаков «+» и «-». Например, в ВМ семейства IBM 360/370/390 для знака «плюс» выбран код 11002= С16, адля знака «минус» — код 11012= D16.
Зонный формат (рис. 2.15, а) применяется в операциях ввода/вывода. В нем под каждую цифру выделяется один байт, где младшие четыре разряда отводятся под код цифры, а в старшую тетраду (поле зоны) записывается специальный код «зона», не совпадающий с кодами цифр и знаков. В IBM 360/370/390 это код 11112= F16. Исключение составляет байт, содержащий младшую цифру десятич­ного числа, где в поле зоны хранится знак числа. На рис. 2.16 показана запись чис­ла -7396 в зонном формате. В некоторых ВМ принят вариант зонного формата, где поле зоны заполняется нулями.
Типы и форматы операндов
69
Байт
i Байт
Байт
Байт
Зона
7
[ Зона
3
Зона
9 Минус
6
1111
0111
( 1 1 1 1
001 1
1111
1001
1 104
0110
Рис, 2.16. Представление числа-7396 в зонном формате
При выполнении операций сложения и вычитания над десятичными числами обычно используется упакованный формат и в нем же получается результат (умно­жение и деление возможно только в зонном формате). В упакованном формате (рис. 2.15, б) каждый байт содержит коды двух десятичных цифр. Правая тетрада последнего байта предназначается для записи знака числа. Десятичное число долж­но занимать целое количество байтов. Если это условие не выполняется, то четыре старших двоичных разряда левого байта заполняется нулями. Так, представление числа -7396 в упакованном формате имеет вид, приведенный на рис. 2.17.
Байт
Байт
Байт
0
7
3
Θ
6
Минус
0000
01 1 1
001 1
1001
0110
1 101
Рис. 2.17. Представление числа-7396 в упакованном формате
Размещение знака в младшем байте, как в зонном, так и в упакованном пред­ставлениях, позволяет задавать десятичные числа произвольной длины и переда­вать их в виде цепочки байтов. В этом случае знак указывает, что байт, в котором он содержится, является последним байтом данного числа, а следующий байт по­следовательности — это старший байт очередного числа.
Числа в форме с плавающей запятой
От недостатков ФЗ в значительной степени свободна форма представления чисел с плавающей запятой (П3), известная также под названиями нормальной или по­лулогарифмической формы. В данном варианте каждое число разбивается на две группы цифр.. Первая группа цифр называется мантиссой, вторая — порядком. Число представляется в виде произведения Х= ±mq±p,me т — мантисса числаX, р — порядок числа, q — основание системы счисления.
Для представления числа в форме с ПЗ требуется задать знаки мантиссы и по­рядка, их модули в q-wmoM коде, а также основание системы счисления (рис. 2.18). Нормальная форма неоднозначна, так как взаимное изменение тир приводит к «плаванию» запятой, чем и обусловлено название этой формы. '
Модуль порядка
Модуль мантиссы
Знакт
Знакр
Р*
Pi
Ро
Ή.,
Л*-2
"ч
Рис. 2.18.Форма представления чисел с плавающей запятой
Диапазон и точность представления чисел с ПТ зависят от числа разрядов, от­водимых под порядок и мантиссу. На рис. 2.19 показаны диапазоны разрядностей порядка и мантиссы, характерные для известных ВМ.
70 Глава 2. Архитектура системы команд
Рис. 2.19.Типовые разрядности полей порядка и мантиссы Помимо разрядности порядка и мантиссы диапазон представления чисел зави­сит и от основания используемой системы счисления, которое может быть отлич­ным от 2. Например, в универсальных ВМ (мэйнфреймах) фирмы IBM использу­ется база 16. Это позволяет при одинаковом количестве битов, отведенных под порядок, представлять числа в большем диапазоне. Так, если поле порядка равно 7 битам, максимальное значение, на которое умножается мантисса, равно 2Ш (при q = 2) или 16ш (при q = 16), адиапазоны представления чисел соответствен­но составят 10"19 <|Х|< 10+|9и1076 <\Х\ < 10+76. Известны также случаи использо­вания базы 8, например, в ВМ В-5500 фирмы Burroughs.
В большинстве вычислительных машин для упрощения операций над поряд­ками последние приводят к целым положительным числам, применяя так называ­емый смещенный порядок. Для этого к истинному порядку добавляется целое по­ложительное число — смещение (рис. 2.20). Например, в системе со смещением 128 порядок -3 представляется как 125 (-3 + 128). Обычно смещение выбирается равным половине представимого диапазона порядков. Отметим, что смещенный порядок занимает все биты поля порядка, в том числе и тот, который ранее ис­пользовался для записи знака порядка.
Смещенный порядок
Модуль мантиссы
Знвкт
Р,
Р»1
...
Р,
Ро
™.1
т#
«ч
Рис. 2.20. Формат числа с ПЗ со смещенным порядком
Типы и форматы операндов 71
Мантисса в числах с ПЗ обычно представляется в нормализованной форме. Это означает, что на мантиссу налагаются такие условия, чтобы она по модулю была меньше единицы (\q\ < 1), а первая цифра после точки отличалась от нуля. Полу­ченная таким образом мантисса называется нормализованной. Для применяемых в ВМ систем счисления можно записать:
ш двоичная: X = q2", (1>|#| = S);
и -восьмеричная: X = q8p, (1 > |?| = ?);
ш -шестнадцатеричная:Х = д16',,(1 >\q\ = 1/16).
Если первые г цифр мантиссы равны нулю, для нормализации ее нужно сдви­нуть относительно запятой на i разрядов влево с одновременным уменьшением порядка на i единиц. В результате такой операции число не изменяется.
База
До нормализации
После нормализации
Порядок
Мантисса
Порядок
Мантисса
2
100
0,000110
001
0,110000
16
8
0,001 хЮ9
6
0,1 xl9"0
В примере для шестнадцатеричной системы после нормализации старшая цифра в двоичном представлении содержит впереди три нуля (0001). Это несколько умень­шает точность представления чисел по сравнению с двоичной системой при оди­наковом числе двоичных разрядов, отведенных под мантиссу.
Если для записи числа с ПЗ используется база 2 (q = 2), то часто применяют еще один способ повышения точности представления мантиссы, называемый при­емом скрытой единицы. Суть его в том, что в нормализованной мантиссе старшая цифра всегда равна единице (для представления нуля используется специальная кодовая комбинация), следовательно, эта цифра может не записываться, а подра­зумеваться. Запись мантиссы начинают с ее второй цифры, и это позволяет задей­ствовать дополнительный значащий бит для более точного представления числа. Следует отметить, что значение порядка в данном случае не меняется. Скрытая единица перед выполнением арифметических операций восстанавливается, а при записи результата — удаляется. Таким образом, нормализованная мантисса 0,101000(1) при использовании способа «скрытой единицы» будет иметь вид 0,010001 (в скобках указана цифра, не поместившаяся в поле мантиссы при стан­дартной записи).
Для более существенного увеличения точности вычислений под число отводят несколько машинных слов, например два. Дополнительные биты, как правило, служат для увеличения разрядности мантиссы, однако в ряде случаев часть из них может отводиться и для расширения поля порядка. В процессе вычислений может получаться ненормализованное число. В таком случае ВМ, если это предписано командой, автоматически нормализует его.
Рассмотренные принципы представления чисел с ПЗ поясним на примере [200]. На рис. 2.21 представлен типичный 32-битовый формат числа с ПЗ. Старший (ле­вый) бит содержит знак числа. Значение смещенного порядка хранится в разрядах
72 Глава 2. Архитектура системы команд
с 1-го по 8-й и может находиться в диапазоне от 0 до 255. Для получения фактичес­кого значения порядка из содержимого этого поля нужно вычесть фиксированное значение, равное 128. С таким смещением фактические значения порядка могут лежать в диапазоне от -128 до +127. В примере предполагается, что основание си­стемы счисления равно 2. Третье поле слова содержит нормализованную мантис­су со скрытым разрядом (единицей). Благодаря такому приему 23-разрядное поле позволяет хранить 24-разрядную мантиссу в диапазоне of 0,5 до 1,0.
8 9
31
Знак мантиссы
Смвщшный порядок
Мантисса
Рис. 2.21.Типичный 32-битовый формат числа с плавающей запятой
На рис. 2.22 приведены диапазоны чисел, которые могут быть записаны с по­мощью 32-разрядного слова.
Представимыв целые числа
Рис. 2.22. Числа, представимыв в 32-битовых форматах: а — целые числа с фиксированной запятой; б —числа с плавающей запятой
В варианте с ФЗ для целых чисел в дополнительном коде могут быть представ­лены все целые числа от -231 до 231 - 1, то есть всего 232 различных чисел (см. рис. 2.22, а). Для случая ПЗ возможны следующие диапазоны чисел (см. рис. 2.22, б):
•   отрицательные числа между -(1 - Тм) х 2127 и -0,5 х 2"128;
•   положительные числа между 0,5 х 2~128 и (1 - 2~24) х 2127.
В эту область не включены пять участков:
•  отрицательные числа, меньшие чем-(1 - 2 24) х2127 — отрицательное пере-
полнение;
Типы и форматы операндов 73
•   отрицательные числа, большие чем -0,5 х 2        — отрицательная потеря зна­чимости;
•   положительные числа, меньшие чем 0,5 х 2~2S — положительная потеря значи­мости;
•  положительные числа, болыпиечем (1 -224)х2127 — положительное переполнение.
Показанная запись числа с ПЗ не учитывает нулевого значения. Для этой цели используется специальная кодовая комбинация. Переполнения возникают, когда в результате арифметической операции получается значение большее, чем можно
(2 х2 -2 ). Потеря значимости — это когда резуль-
г ~                                                                                   г                                               /П-120          ^-100           ^-230 \
тат представляет собой слишком маленькое дробное значение (2 х2 =2 ). Потеря значимости является менее серьезной проблемой, поскольку такой резуль­тат обычно рассматривают как нулевой.
Следует также отметить, что числа в форме с ПЗ, в отличие от чисел в форме с ФЗ, размещены на числовой оси неравномерно. Возможные значения в начале числовой оси расположены плотнее, а по мере движения вправо — все реже (рис. 2.23). Это означает, что многие вычисления приводят к результату, который не является точным,.то есть представляет собой округление до ближайшего значе­ния, представимого в данной форме записи.
О                  п                                  пх2
Рис. 2.23. Плотность чисел с плавающей запятой на числовой оси
п х4
Для формата, изображенного на рис. 2.21, имеет место противоречие между диа­пазоном и точностью. Если увеличить число битов, отведенных под порядок, рас­ширяется диапазон пред ставимых чисел. Однако, Поскольку может быть представ­лено только фиксированное число различных значений, уменьшается плотность и тем самым точность. Единственный путь увеличения как диапазона, так и точ­ности — увеличение количества разрядов, поэтому в большинстве ВМ предлагает­ся использовать числа в одинарном и двойном форматах. Например, число оди­нарного формата может занимать 32 бита, адвойного — 64 бита.
Числа с плавающей запятой в разных ВМ имеют несколько различных форма­тов. В табл. 2.5 приводятся основные параметры для нескольких систем представ­ления чисел в форме с ПЗ. В настоящее время для всех ВМ рекомендован стан­дарт, разработанный общепризнанным международным центром стандартизации IEEE (Institute of Electrical and Electronics Engineers).
Таблица 2.5. Варианты форматов чисел с плавающей запятой1
Параметр
IBM 390
VAX
IEEE 794
Длина слова(биГ)
0:32; Д: 64
0:32; Д: 64
0:32; Д: 64
Порядок(бит)
7 бит
8 бит
0;8;Д:11
продолжение &
10 — одинарный формагг; Д — двойной формат.
74 Глава 2. Архитектура системы-команд Таблица 2.5 продолжение)
Параметр
IBM 390
VAX
IEEE 754
Мантисса (F)
0:6 цифр; Д: 14 цифр
О: (1) +23 бита Д:(1) + 55бит
0:{1) + 23бита Д:(1)+52бита
Смещение порядка
64
128
К: 127; Д: 1023
База
16
2
2 ·
Скрытая 1
Нет
Да
Да
Запятая
Слева от мантиссы
Слева от скрытой 1
Справа старшего бита мантиссы
Диапазон F
(1,16)£F<1
0,5£F<1
1£F<2
Представление F
Величина со знаком
Величина со знаком
Величина со знаком
Максимальное полож ител ьное
число
1663=1076
2126=1038
21 024= 10 308 (Д)
Точность
0:16-*ξ1(Γ7 Д: 16" = 10"
0:2"и = 10~7
0:2"и = 10 7
Λ2·*ϊ10""
Стандарт IEEE754
Рекомендуемый для всех ВМ формат представления чисел с плавающей запятой определен стандартом IEEE 754. Этот стандарт был разработан с целью облегчить перенос программ с одного процессора на другие и нашел широкое применение практически во всех процессорах и арифметических сопроцессорах.
Рис. 2.24. Основные форматы IEEE754: а — одинарный; б —двойной Стандарт определяет 32-битовый (одинарный) и 64-битовый (двойной) фор­маты (рис. 2.24) с 8- и 11-разрядным порядком соответственно. Основанием сис­темы счисления является 2. В дополнение, стандарт предусматривает два расши­ренных формата, одинарный и двойной, фактический вид которых зависит от конкретной реализации. Расширенные форматы предусматривают дополнитель-
Типы и форматы операндов 75
ные биты для порядка (увеличенный диапазон) и мантиссы (повышенная точ­ность) . Таблица 2.6 содержит описание основных характеристик всех четырех фор­матов.
Не все кодовые комбинации в форматах ШЕЕ интерпретируются обычным путем — некоторые комбинации используются для представления специальных значений. Предельные значения порядка, содержащие все нули (0) и все единицы (255 — в одинарном формате и 2047 — в двойном формате), определяют специаль­ные значения.
Таблица 2.6. Параметры форматов стандарта ΙΕΕΕ754
Параметр
Формат
одинарный
одинарный расширенный
двойной
двойной расширенный
Ширина слова, бит
32
i43
64 ■
i79
Ширина порядка, бит..
8
ill
11
il5
. Смещение порядка
127
Не определено
1023
Не определено
Максимальный порядок
127
> 1023
1023
> 16 383
Минимальный порядок
-126
<:-1022
-1022
<:-16382
Диапазон чисел
КГ38,10+38
Не определен
10ш
Не определен
Длина мантиссы, бит
23
i31
52
i63
Количество порядков
254
Не определено
2046
Не определено
Количество мантисс
223
Не определено
252
Не определено
Количество значений
1,98 х231
Не определено
1,99 х 263
Не определено
Представлены следующие классы чисел: Ш Порядки в диапазоне от 1 до 254 для одинарного формата и от 1 до 2036 — для двойного формата, используются для представления ненулевых нормализован­ных чисел. Порядки смещены так, что их диапазон составляет от -126 до +127 для одинарного формата и от -1022 до +1023 — для двойного формата. Норма­лизованное число требует, чтобы слева от двоичной запятой был единичный бит. Этот бит подразумевается, благодаря чему обеспечивается эффективная ширина мантиссы, равная 24 битам для одинарного и 53 битам — для двойного форматов.
ш Нулевой порядок совместно с нулевой мантиссой представляют положитель­ный или отрицательный 0, в зависимости от состояния бита знака мантиссы.
Ш Порядок, содержащий единицы во всех разрядах, совокупно с нулевой мантис­сой представляют положительную или отрицательную бесконечность, в зави­симости от состояния бита знака, что позволяет пользователю самому решить, считать ли это ошибкой или продолжать вычисления со значением, равным бесконечн ости.
76 Глава 2. Архитектура системы команд
•   Нулевой порядок в сочетании с ненулевой мантиссой представляют ненорма­лизованное число. В этом случае бит слева от двоичной точки равен 0 и факти­ческий порядок равен -126 или -1022. Число является положительным или отрицательным в зависимости от значения знакового бита.
•   Кодовая комбинация, в которой порядок содержит все единицы, а мантисса не равна 0, используется как признак «не числа» (NAN — Not a Number) и служит для предупреждения о различных исключительных ситуациях.
Упакованные числа с плавающей запятой
В последних версиях АСК, предусматривающих особые команды для обработки мультимедийной информации, помимо упакованных целых чисел используются и упакованные числа с плавающей запятой. Так, в уже упоминавшейся техноло­гии 3DNow! фирмы AMD имеются команды, служащие для увеличения произво­дительности систем при обработке трехмерных приложений, описываемых числа­ми с ПЗ. Каждая такая команда работает с двумя операндами с плавающей запятой одинарной точности. Операнды упаковываются в 64-разрядные группы, как это ■ показано на рис. 2.25.
Технология 3DNow!. Упакованные числа с плавающей запятой (2x32 бит)
Рис. 2.25. Формат упакованных чисел с плавающей запятой в технологиях 3DNow!, SSE, SSE2
В микропроцессорах фирмы Intel, начиная с Pentium III, для аналогичных це­лей поддержаны команды, реализующие технологию SSE, также ориентирован­ную на параллельную обработку упакованных чисел с ПЗ. Здесь числа объеди­няются в группы длиной 128 бит, и это позволяет упаковать в группу четыре 32-разрядных числа с ПЗ (числа с одинарной точностью). Позже, в технологии SSE2, которую можно считать дальнейшим развитием SSE, появился формат, где в группу из 128 бит упаковываются два 64-разрядных числа с ПЗ, то есть числа, представленные с двойной точностью.
Разрядность основных форматов числовых данных
Данные, представляющие в ВМ числовую информацию, могут иметь фиксирован­ную или переменную длину. Операционные устройства вычислительных машин (целочисленные арифметико-логические устройства, блоки обработки чисел
Типы и форматы операндов
77
с плавающей запятой, устройства десятичной арифметики и т. п.), как правило, рас­считаны на обработку кодов фиксированной длины. Общепринятые величины раз­рядности кодов чисел показаны на рис. 2.26.
Рис. 2.26. Стандартная длина фиксированных форматов представления чисел
Наименьшей единицей данных в ВМ служит бит (BIT, Binary digiT — двоич­ная цифра). В большинстве случаев эта единица информации слишком мала. Од­нобитовые операционные устройства использовались в ВМ с последовательной обработкой информации, а в современных машинах с параллельной обработкой разрядов они практически не применяются. Побитовую работу с данными скорее можно встретить в многопроцессорных вычислительных системах, построенных из одноразрядных процессоров.
Следующая по величине единица состоит из четырех битов и называется полу­байтом или тетрадой, или реже «ниблом» (nibble — огрызок). Она также редко имеет самостоятельное значение и заслуживает упоминания как единица представления отдельных десятичных цифр при их двоично-десятичной записи.
Реально наименьшей обрабатываемой единицей считается байт, состоящий из восьми битов. На практике эта единица информации также оказывается недоста­точной, и значительно чаще применяются числа, представленные двумя (полусло­во), четырьмя (слово), восемью (двойное слово) или шестнадцатью (счетверенное слово) байтами1.
Разрядность целочисленного АЛУ обычно выбирается равной ширине адреса (для большинства современных ВМ это 32 разряда). Следовательно, наиболее выгодными в плане быстродействия являются такие целые числа, длина которых
1 Согласно терминологии Intel. В другом варианте (DEC) естественный размер слова — 2 байта, двой­ного или длинного слова (longword) — 4 байта и упоминавшегося выше квадрослова (quadword) — 8 байт.
78 Глава 2. Архитектура системы команд
совпадает с разрядностью адреса. Использование более коротких чисел позволяет сэкономить на памяти, но выигрыша в производительности не дает.
Блоки операций с плавающей запятой обычно согласованы со стандартом IEEE 754 и рассчитаны на обработку чисел в формате двойной длины (64 бита), , В большинстве ВМ реальная разрядность таких блоков даже больше (80 бит). Та­ким образом, наилучшим вариантом при проведении вычислений с плавающей запятой можно считать формат двойного слова. При выборе формата меньшей' длины (32 разряда) вычисления все равно ведутся с большей точностью, после чего ; результат округляется. Таким образом, использование короткого формата чисел с плавающей запятой, как и в случае целых чисел с фиксированной запятой, поми- ■ мо экономии памяти никаких иных преимуществ также не дает.
В работе [120] приводятся усредненные данные о частоте использования ос­новных форматов чисел, полученные в ходе выполнения пакета тестовых программ/ SPEC92 на вычислительной машине DEC VAX (рис. 2.27).
Рис. 2.27. Частота обращения к числовым данным в зависимости от их разрядности
В приложениях, оперирующих десятичными числами, где количество цифр в числе может варьироваться в широком диапазоне, что характерно для задач из области экономики, более удобными оказываются форматы переменной длины. В этом случае числа не переводятся в двоичную систему, а записываются в виде последовательности двоично-кодированных десятичных цифр. Длина подобной цепочки может быть произвольной, а для указания ее границы обычно использу­ют символ-ограничитель, код которого не совпадает с кодами цифр. Длина цифро­вой последовательности может быть задана явно в виде количества цифр числа и храниться в первом байте записи числа, однако этот прием более характерен для' указания длины строки символов.
Размещение числовых данных в памяти                                 -\
В современных ВМ разрядность одной ячейки памяти, как правило, равна одному | байту (8 бит). В то же время реальная длина кодов чисел составляет 2, 4, 8 или \ 16 байт. При хранении таких чисел в памяти последовательные байты числа раз* 1
Типы и форматы операндов 79
мещают в нескольких ячейках с последовательными адресами, при этом для дос­тупа к числу указывается только наименьший из адресов. При разработке архи­тектуры системы команд необходимо определить порядок размещения байтов в па­мяти, то есть какому из байтов (старшему или младшему) будет соответствовать этот наименьший адрес1. На рис. 2.28 показаны оба варианта размещения 32-раз­рядного числа в четырех последовательных ячейках памяти, начиная с адресах.
Рис. 2.28. Размещение в памяти 32-разрядного числа: а — начиная со старшего байта;
б — начиная с младшего байта
В вычислительном плане оба способа записи равноценны. Так, фирмы DEC и Intel отдают предпочтения размещению в первой ячейке младшего байта, a IBM и Motorola ориентируются на противоположный вариант. Выбор обычно связан с некими иными соображениями разработчиков ВМ. В настоящее время в боль-. шинстве машин предусматривается использование обоих вариантов, причем вы­бор может быть произведен программным путем за счет соответствующей уста­новки регистра конфигурации.
1 В англоязычной литературе систему записи числа, начиная со старшего байта, обозначают термином «big endian», а с младшего байта — термином «little endian». Оба названия происходят от названия племен («тупоконечники* и «остроконечники»), упоминаемых в книге Джонатана Свифта «Путеше­ствия Гулливера». Там описывается религиозная война между этими племенами, по причине разно­гласий в вопросе, с какого конца следует разбивать Яйцо — тупого или острого.
80 Глава 2. Архитектура системы команд
Помимо порядка размещения байтов, существенным бывает и выбор адреса, с которого может начинаться запись числа. Связано это с физической реализаци­ей полупроводниковых запоминающих устройств, где обычно предусматривается возможность считывания (записи) четырех байтов подряд. Причем данная опера­ция выполняется быстрее, если адрес первого байта.4 отвечает условию A mod 5 = 0 (S = 2, 4, 8, 16). Числа, размещенные в памяти в соответствии с этим правилом, называются выравненными (рис. 2.29).
На рис. 2.30 показаны варианты размещения 32-разрядного слова без выравни­вания. Их использование может приводить к снижению производительности.
Рис. 2.30. Размещение 32-разрядного слова без соблюдения правила выравнивания
Большинство компиляторов генерируют код, в котором предусмотрено вырав- ■ нивание чисел в памяти.
Символьная информация
В общем объеме вычислительных действий все большая доля приходится на об­работку символьной информации, содержащей буквы, цифры, знаки препинания, математические и другие символы. Каждому символу ставится в соответствие оп­ределенная двоичная комбинация. Совокупность возможных символов и назна-: ченных им двоичных кодов образует таблицу кодировки. В настоящее время при- . меняется множество различных таблиц кодировки. Объединяет их весовой принцип, при котором веса кодов цифр возрастают по мере увеличения цифры, а веса символов увеличиваются в алфавитном порядке. Так вес буквы «Б» на еди- ■> нипу больше веса буквы «А». Это способствует упрощению обработки в ВМ. h До недавнего времени наиболее распространенными были кодовые таблицы, j в которых символы кодируются с помощью восьмиразрядных двоичных комбина-1 ций (байтов), позволяющих представить 256 различных символов:                       1
•   расширенный двоично-кодированный код EBCDIC (Extended Binary Coded,j Decimal Interchange Code);                                                                            j
•   американский стандартный код для обмена информацией ASCII (American ;
Standard Code for Information Interchange).                                                  . 1
Код EBCDIC используется в качестве внутреннего кода в универсальных ВМ j фирмы IBM. Он же известен под названием ДКОИ (двоичный код для обработки ; информации).                                                                                                     ■
Стандартный код ASCII—7-разрядный, восьмая позиция отводится для записи ; бита четности. Это обеспечивает представление 128 символов, включая все j
Типы и форматы операндов 81
латинские буквы, цифры, знаки основных математических операций и знаки пун­ктуации. Позже появилась европейская модификация ASCII, называемая Latin 1 (стандарт ISO 8859-1). В ней «полезно» используются все 8 разрядов. Дополни­тельные комбинации (коды 128-255) в новом варианте отводятся для представле­ния специфических букв алфавитов западно-европейских языков, символов псев­дографики, некоторых букв греческого алфавита, а также ряда математических и финансовых символов. Именно эта кодовая таблица считается мировым стан­дартом де-факто, который применяется с различными модификациями во всех стра­нах. В зависимости от использования кодов 128-255 различают несколько вари­антов стандарта ISO 8859 (табл. 2.7).
Таблица 2.7. Варианты стандарта ISO 8859
Стандарт
Характеристика
ISO 8859-1
Западно-европейские языки
ISO 8859:2
Языки стран центральной и восточной Европы
ISO 8859-3
Языки стран южной Европы, мальтийский и эсперанто
ISO 8859-4
Языки стран северной Европы
ISO 8859-5
Языки славянских стран с символами кириллицы
, ISO 8859-6
Арабский язык
ISO 8859-7
Современный греческий язык
ISO 8859-8
Языки иврит и идиш
ISO 8859-9
Турецкий язык
ISO 8859-10
Языки стран северной Европы (лапландский, исландский) '
ISO 8859-11
Тайский язык
ISO 8859-13
Языки балтийских стран
ISO 8859-14
Кельтский язык
ISO 8859-15
Комбинированная таблица для европейских языков
ISO 8859-16
Содержит специфические символы ряда языков: албанского, хорватского, английского, финского, французского, немецкого, венгерского, ирландского, итальянского, польского, румынского и словенского
В популярной в свое время операционной системе MS-DOS стандарт ISO 8859 реализован в форме кодовых страниц OEM (Original Equipment Manufacturer). Каждая OEM-страница имеет свой идентификатор (табл. 2.8).
Таблица 2.8. Наиболее распространенные кодовые страницы OEM
Идентификатор
Страны
кодовой страницы
СР437
США, страны западной Европы и Латинской Америки
СР708
Арабские страны .. Λ
I----------------------------------------------------------------------------продолжение &
82 Глава 2. Архитектура системы команд
Таблица 2.8 (продолжение)
Идентификатор
Страны
кодовой страницы
СР737
Греция
СР775 .
Латвия, Литва, Эстония
СР852
Страны восточной Европы -
СР853
Турция
СР855
Страны с кириллической письменностью
СР860
Португалия
СР862
Израиль
СР865
Дания, Норвегия
СР866
Россия
СР932
Япония
СР936
Китай
Хотя код ASGII достаточно удобен, он все же слишком тесен и не вмещает мно­жества необходимых символов. По этой причине в 1993 году консорциумом ком­паний Apple Computer, Microsoft, Hewlett-Packard, DEC и IBM был разработан 16-битовый, стандарт ISO 10646, определяющий универсальный набор символов (UCS, Universal Character Set). Новый код, известный под названием Unicode, позволяет задать до 65 5 36 символов, то есть дает возможность одновременно пред­ставить символы всех основных «живых» и «мертвых» языков. Для букв русского языка выделены коды 1040-1093.
В «естественном» варианте кодировки Unicode, известном как UCS-2, каждый символ описывается двумя последовательными байтами тип, так что номеру сим­вола соответствует численное значение 256хт + п. Таким образом, кодовый но­мер представлен 1 б-разряднымдвоичным числом. Наряду с UCS-2 в рамках Unicode существуют еще несколько вариантов кодировки Unicode (UTF, Unicode Transfor­mation Formats), основные из которых UTF-8 и UTF-7.
В кодировке UTF-8 коды символов меньшие, чем 128, представляются одним байтом. Все остальные коды формируются по более сложным правилам. В зависи­мости от символа его код может занимать от двух до шести байтов, причем стар­ший бит каждого байта всегда имеет единичное значение. Иными словами, значе­ние байта лежит в диапазоне от 128 до 255. Ноль в старшем бите байта означает, что код занимает один байт и совпадает по кодировке с ASCII. Схема формирова­ния кодов UTF-8 показана в табл. 2.9.
Таблица 2.9. Структура кодов UTF-8
Число байтов
Двоичное представление
Число свободных битов
1
Оххххххх
7
2
110ххххх 10хххххх
1 11(5 + 6)
Типы и форматы операндов 83
Число байтов
Двоичное представление
Число свободных битов
3
110хххх1 Охххххх 10хххххх
16(4 + 6x2)
4
1111 Оххх 10хххххх 10хххххх 10хххххх
21(3 + 6x3) .
5
11111 Охх 10хххххх 10хххххх 10хххххх 10хххххх
26(2 + 6x4)
6
1111110x1 Охххххх 10хххххх 10хххххх 10хххххх 10хххххх
31(1+6x5)
В UTF-7 код символа также может занимать один или более байтов, однако в каждом из байтов значение не.превышает 127 (старший бит байта содержит ноль). Многие символы кодируются одним байтом, и их кодировка совпадает с ASCII, однако некоторые коды зарезервированы для использования в качестве преамбу­лы, характеризующей последующие байты многобайтового кода.
Стандарт Unicode обратно совместим с кодировкой ASCII, однако если в ASCII для представления схожих по виду символов (минус, тире, знак переноса) приме­нялся общий код, в Unicode каждый из этих символов имеет уникальную кодировку. Впервые Unicode был использован в операционной системе Windows NT. Распре­деление кодов в Unicode иллюстрирует табл. 2.10.
Таблица 2.10. Блоки символов в стандарте Unicode
Коды
Символы
0-8191
Алфавиты — английский, европейские, фонетический, кириллица, армянский, иврит, арабский, эфиопский, бенгали, деванагари, гур, гуджарати, ория, телугу, тамильский, каннада, малайский, сингальский, грузинский, тибетский, тайский, лаосский, кхмерский, монгольский
8192-12287
Знаки пунктуации, математические операторы, технические ' символы, орнаменты и т. п.
12288-16383
Фонетические символы китайского, корейского и японского языков
16384-59391
Китайские, корейские, японские идеографы. Единый набор символов каллиграфии хань
59392-65024
Блок для частного использования
65025-65536
Блок обеспечения совместимости с программным обеспечением
Параллельно с развитием Unicode исследовательская группа ISO проводит ра­боты над 32-битовой кодовой таблицей, однако ввиду широкой распространенно­сти кодировки Unicode дальнейшие перспективы новой разработки представля­ются неопределенными.
Логические данные
Элементом логических данных является логическая (булева) переменная, кото­рая может принимать лишь два значения: «истина» или «ложь». Кодирование ло­гического значения принято осуществлять битом информации: единицей кодируют
84 Глава 2. Архитектура системы команд
истинное значение, нулем — ложное. Как правило, в ВМ оперируют наборами ло­гических переменных длиной в машинное слово. Обрабатываются такие слова с помощью команд логических операций (И, ИЛИ, НЕ и т. д.), при этом все биты обрабатываются одинаково, но независимо друг от друга, то есть никаких перено- ? сов между разрядами не возникает.
Строки
Строки — это непрерывная последовательность битов, байтов, слов или двойных слов. Битовая строка может начинаться в любой позиции байта и содержать до 1 232 бит. Байтовая строка может состоять из байтов, слов или двойных слов. Длина такой строки варьируется от нуля до 232 - 1 байт (4 Гбайт). Приведенные цифры характерны для превалирующих в настоящее время 32-разрядных ВМ.
Если байты байтовой строки представляют собой коды символов, то говорят ', о текстовой строке. Поскольку длина текстовой строки может меняться в очень широких пределах, то для указания конца строки в последний байт заносится код-ограничитель — обычно это нули во всех разрядах байта. Иногда вместо ограничите­ля длину строки указывают числом, расположенным в первом байте (двух) строки.
Прочие виды информации
Представляемая в ВМ информация может быть статической или динамической [33]. Так, числовая, символьная и логическая информация является статической — ее значение не связано со временем. Напротив, аудиоинформация имеет динами­ческий характер — существует только в режиме реального времени и не может быть остановлена для более подробного изучения. Если изменить масштаб времени, аудиоинформация искажается, что используется, например, для создания звуко­вых эффектов.
Видеоинформация
Видеоинформация бывает как статической, так и динамической. Статическая ви­деоинформация включает в себя текст, рисунки, графики, чертежи, таблицы и др. Рисунки делятся также на плоские — двумерные и объемные — трехмерные.
Динамическая видеоинформация — это видео-, мулы- и слайд-фильмы. В их основе лежит последовательное экспонирование на экране в реальном масштабе времени отдельных кадров в соответствии со сценарием. Динамическая информа­ция используется либо для передачи движущихся изображений (анимация), либо для последовательной демонстрации отдельных кадров (слайд-фильмы).
Для демонстрации анимационных и слайд-фильмов опираются на различные принципы. Анимационные фильмы демонстрируются так, чтобы зрительный ап­парат человека не мог зафиксировать отдельных кадров (для получения качествен­ной анимации кадры должны сменяться порядка 70 раз/с). При демонстрации слайд-фильмов каждый кадр.экспонируется на экране столько времени, сколько необходимо для восприятия его человеком (обычно от 30 с до 1 мин). Слайд-филь­мы можно отнести к статической видеоинформации.
В вычислительной технике существует два способа представления графичес­ких изображений: матричный (растровый) и вектпорный. Матричные (bitmap) форматы хорошо подходят для изображений со сложными гаммами цветов, оттен-
Типы и форматы операндов 85
ков и форм, таких как фотографии, рисунки, отсканированные данные. Векторные форматы более приспособлены для чертежей и изображений с простыми форма­ми, тенями и окраской.
В матричных форматах изображение представляется прямоугольной матрицей точек — пикселов (picture element), положение которых в матрице соответствует координатам точек на экране. Помимо координат каждый пиксел характеризуется своим цветом, цветом фона или градацией яркости. Количество битов, выделяе­мых для указания цвета пиксела, изменяется в зависимости от формата. В высоко­качественных изображениях цвет пиксела описывают 24 битами, что дает около 16 млн цветов. Основной недостаток матричной (растровой) графики заключает­ся в большой емкости памяти, требуемой для хранения изображения, из-за чего для описания изображений прибегают к различным методам сжатия данных. В на­стоящее время существует множество форматов графических файлов, различаю­щихся алгоритмами сжатия и способами представления матричных изображений, а также сферой применения. Некоторые из распространенных форматов матрич­ных графических файлов перечислены в табл. 2.11.
Таблица 2.11. Матричные графические форматы
Обозначение
Полное название
BMP
Windows и OS\2 Bitmap
GIF
Graphics Interchange Format
PCX
PC Paintbrush File Format
JPEG
Joint Photographic Experts Group
TIFF
Tagged Image File Format
PNG
Portable Network Graphics
Векторное представление, в отличие от матричной графики, определяет описа­ние изображения не пикселами, а кривыми — сплайнами. Сплайн — это гладкая кривая, которая проходит через две или более опорные точки, управляющие фор­мой сплайна. В векторной графике наиболее распространены сплайны на основе кривых Безье. Суть сплайна: любую элементарную кривую можно построить, зная четыре коэффициента Р0, Р„ Р2 и Р3, соответствующие четырем точкам на плоско­сти. Перемещение этих точек влечет за собой изменение формы кривой (рис. 2.31).
86 Глава 2. Архитектура системы команд
Хотя это может показаться более сложным, но для многих видов изображений использование математических описаний является более простым способом. В век­торной графике для описания объектов используются математические формулы. Это позволяет при рисовании объектов вычислять, куда необходимо помещать реальные точки изображения. Имеется ряд простейших объектов, или примити­вов, например эллипс, прямоугольник, линия. Эти примитивы и их комбинации служат основой для создания более сложных изображений. В простейшем случае изображение может быть составлено из отрезков линий, для которых задаются на­чальные координаты, угол наклона, длина, толщина линии, цвет линии и цвет фона.
Основное достоинство векторной графики — описание объекта, является про­стым и занимает мало памяти. Кроме того, векторная графика в сравнении с мат­ричной имеет следующие преимущества:
Ш. простота масштабирования изображения без ухудшения его качества;
К независимость емкости памяти, требуемой для хранения изображения, от вы­бранной цветовой модели.
Недостатком векторных изображений является их некоторая искусственность, заключающаяся в том, что любое изображение необходимо разбить на конечное множество составляющих его примитивов. Как и для матричной графики, суще­ствует несколько форматов графических векторных файлов. Некоторые из них приведены в табл. 2.12.
Таблица 2.12. Векторные графические форматы
Обозначение
Полное название
DXF
Drawing Interchange Format
CDR
Corel Drawing
HPGL
Hewlett-Packard Graphics Language
PS
PostScript
SVG
Scalable Vector Graphics
VSD
Microsoft Visio format
Матричная и векторная графика существуют не обособленно друг от друга. Так, векторные рисунки могут включать в себя и матричные изображения. Кроме того, векторные и матричные изображения могут быть преобразованы друг в друга. Гра­фические форматы, позволяющие сочетать матричное и векторное описание изоб­ражения, называются метафайлами. Метафайлы обеспечивают достаточную ком­пактность файлов с сохранением высокого качества изображения.
Таблица 2.13. Форматы метафайлов
Обозначение
Полное название
EPS
Encapsulated PostScript
WMF
Windows Metafile
CGM
Computer Graphics Metafile
Типы команд 87
Рассмотренные формы представления статической видеоинформации исполь­зуются, в частности, для отдельных кадров, образующих анимационные фильмы. Для хранения анимационных фильмов применяются различные методы сжатия информации, большинство из которых стандартизовано,.
Аудиоинформация
Понятие аудио связано со звуками, которые способно воспринимать человеческое ухо. Частоты аудиосигналов лежат в диапазоне от 15 Гц до 20 КГц, а сигналы по своей природе являются непрерывными (аналоговыми). Прежде чем быть пред-' ставленной в ВМ, аудиоинформация должна быть преобразована в цифровую форму (оцифрована). Для этого значения звуковых сигналов (выборки, samples), взятые через малые промежутки времени, с помощью аналого-цифровых преобра­зователей (АЦП) переводятся в двоичный код. Обратное действие выполняется цифро-аналоговыми преобразователями (ЦАП). Чем чаще производятся выборки, тем выше может быть точность последующего воспроизведения исходного сигнала, но тем большая емкость памяти требуется для хранения оцифрованного звука.
Цифровой эквивалент аудиосигналов обычно хранится в виде файлов, причем широко используются различные методы сжатия такой информации. Как прави­ло, к методам сжатия аудиоинформации предъявляется требование возможности восстановления непрерывного сигнала без заметного ухудшения его качества. В на­стоящее время распространен целый ряд форматов хранения аудиоинформации. Некоторые из них перечислены в табл. 2.14.
Таблица 2.14. Форматы аудиофайлов
Обозначение
Полное название
AVI
Audio Yideo Interleave
W
WAVeform Extension.
MIDI
Musical Instrument Digital Interface
AIF
Audio Interchange Format
MPEG
Motion Picture Expert Group Audio
RA
Real Audio
Типы команд
Несмотря на различие в системах команд разных ВМ, некоторые основные типы операций могут быть найдены в любой из них. Для описания этих типов примем следующую классификацию:
и   · команды пересылки данных;
ш   · команды арифметической и логической обработки;
■   · команды работы со строками;
ш   · команды SIMD;
ш   · команды преобразования;
Hosted by uCoz